Regenerative or Hopkinson’s test on d.c machines:
Regenerative or Hopkinson’s test on dc machines is useful to determine the efficiency which the power.This method of determining the efficiency of a d.c. machine saves power and gives more accurate results. In order to carry out this test, we require two identical d.c. machines and a source of electrical power.
Regenerative or Hopkinson’s test Working Principle:
Two identical d.c. shunt machines are mechanically coupled and connected in parallel across the d.c. supply. By adjusting the field excitation of the machines,one is run as a motor and the other as a generator.The electric power from the generator and electrical power from the d.c. supply are fed to the motor. The electric power given to the motor is mostly converted into mechanical power, the rest going to the various motor losses.
This mechanical power is given to the generator. The electrical power of the generator is given to the motor except that which is wasted as generator losses. Thus the electrical power taken from the d.c. supply is the sum of motor and generator losses and this can be measured directly by a voltmeter and an ammeter. Since the power input from the d.c. supply is equal to the power required to supply the losses of the two machines, this test can be carried out with a small amount of power.
By adjusting the field strengths of the machines, any load can be put on the machines. Therefore, we can measure the total loss of the machines at any load. Since the machines can be tested under full-load conditions (of course at the expense of power equal to the losses in the two machines), the temperatures rise and commutation qualities of the machines can be observed.This is the working principle of Regenerative or Hopkinson’s test.
Regenerative or Hopkinson’s test Circuit:
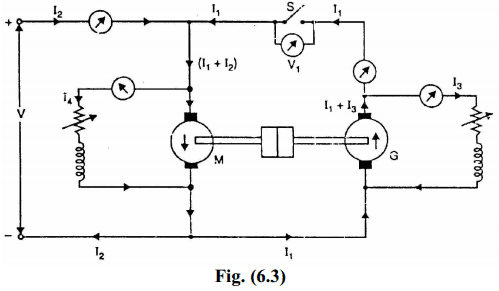
The below figure shows the essential connections for Hopkinson’s test.Two identical d.c. shunt machines are mechanically coupled and are connected in parallel across the d.c. supply.By adjusting the field strengths of the two machines, the machine M is made to run as a motor and machine G as a generator. The motor M draws current I1 from the generator G and current I2 from the d.c. supply so that input current to motor M is (I1 + I2). Power taken from the d.c. supply is VI2 and is equal to the total motor and generator losses. The field current of motor M is I4 and that of generator G is I3.
If V be the supply voltage, then,
Motor input = V(I1 + I2)
Generator output = VI1
We shall find the efficiencies of the machines considering two cases viz.
(i) assuming that both machines have the same efficiency
(ii) assuming iron, friction and windage losses are the same in both machines.
(i) Assuming that both machines have the same efficiency
This expression gives the value of efficiency sufficiently accurate for a rough test. However, if accuracy is required, the efficiencies of the two machines
should be calculated separately as below.
(ii) Assuming that iron, friction and windage losses are same in
both machines.
It is not to assume that the two machines have the same efficiency. It is because armature and field in the two machines are not the same.However , iron , friction and windage losses in the two machines will be the same because the machines are identical.On this assumption, we can find the of each machine as under:
Hopkinson’s Test Advantages:
The advantages of Hopkinson’s test are :
(i) The total power required to test the two machines is small compared
with the full-load power of each machine.
(ii) The machines can be tested under full-load conditions so that
commutation qualities and temperature rise can be checked.
(iii) It is more accurate to measure the loss directly than to measure it as the
difference of the measured input and output.
(iv) All the measurements are electrical which are simpler and more accurate
than mechanical measurements.
Hopkinson’s Test Disadvantages:
- The main disadvantage is that two similar d.c. machines are required.