MMF method for determining voltage regulation of Alternator:
MMF method is used for determining the voltage regulation of an alternator or synchronous generator is also called Ampere turns method or Rothert’s MMF method. This MMF method is based on the results of open circuit test and short circuit test on an alternator. For any synchronous generator or alternator, MMF is required, which is a product of field current and turns of the field winding for two separate purposes.
1. It must have an MMF necessary to induce the rated terminal voltage on the open circuit.
2. It must have an MMF equal and opposite to that of armature reaction MMF.
Key Point: In most of the cases, as the number of turns on the field winding is not known, the MMF is calculated and expressed in terms of the field current itself.
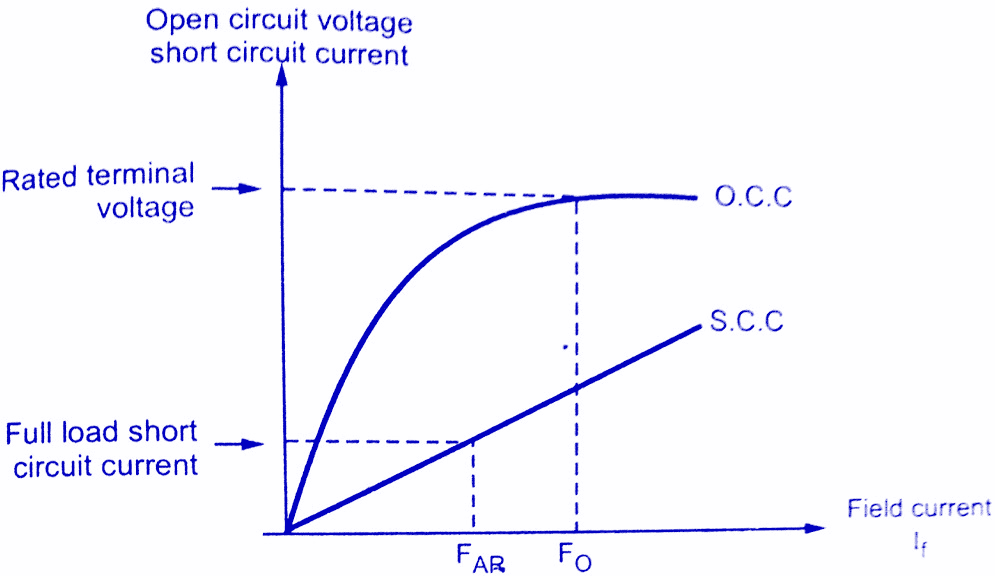
The field mmf which is required for inducing the rated terminal voltage on the open circuit can be obtained from open circuit test results and open circuit characteristics. This is denoted as FO.
Synchronous impedance consists of two components. They are armature resistance and synchronous reactance. Now synchronous reactance also has two components, armature leakage reactance and armature reaction reactance. In the short-circuit test, field MMF is necessary to overcome drop across armature resistance and leakage reactance and also to overcome the effect of armature reaction.
This textbook “Electrical Machinery by P.S. Bhimbhra” is the best in industry. Grab it now for very less price.
But drop across armature resistance and leakage reactance is very small and can be neglected. Thus in short circuit test, field MMF circulates the full load current balancing the armature reaction effect. The value of ampere-turns required to circulate full load current can be obtained from short circuit characteristics. This is denoted as FAR.
Under short circuit condition as resistance and leakage reactance of armature has no significant role, the armature reactance is dominating and hence the power factor of the purely reactive circuit is zero lagging. Hence FAR gives demagnetising ampere-turns. Thus the field MMF is entirely used to overcome the armature reaction which is wholly demagnetising in nature.
The two components of total field mmf which are FO and FAR are indicated in OCC(open circuit characteristics) and SCC (short circuit characteristics) as shown in the below figure.
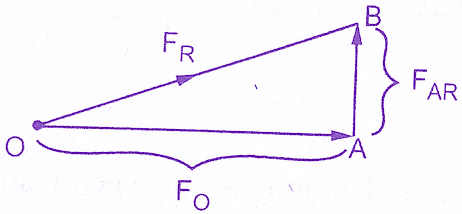
If the alternator is supplying full load, then total field MMF is the vector sum of its two components Fo and FAR. This depends on the power factor of the load which alternator is supplying. The resultant field MMF is denoted as FR. Let us consider the various power factors and the resultant FR.
Zero lagging p.f : As long as the power factor is zero lagging, the armature reaction is completely demagnetising. Hence the resultant FR is the algebraic sum of the two components FO and FAR. Field MMF method is not only required to produce rated terminal voltage but also required to overcome completely demagnetising armature reaction effect. It is shown if the below figure.
OA = FO
AB = FAR DEMAGNETISING
OB = FR = FO + FAR
Total field MMF is greater than Fo
Zero leading p.f : When the power factor is zero leading then the armature reaction is totally magnetising and helps main flux to induce rated terminal voltage. Hence net field required is less than that required to induce rated voltage normally, as part of its function is done by magnetising armature reaction component. The net field mmf in this MMF method is the algebraic difference between the two components FO and FAR.
OA = FO
AB = FAR MAGNETISING
OB = FO – FAR = FR
Total MMF is less than FO.
Unity p.f : Under unity power factor condition, the armature reaction is cross magnetising and its effect is to distort the main flux. Thus FO and FAR are at right angles to each other and hence resultant MMF is the vector sum of FO and FAR in this MMF method.This is shown in the below figure.
OA = FO
AB = FAR CROSS MAGNETISING
OB = FR = FO + FAR
Here below is the following considerations for MMF or Ampere turn method for determining voltage regulation of Alternator.
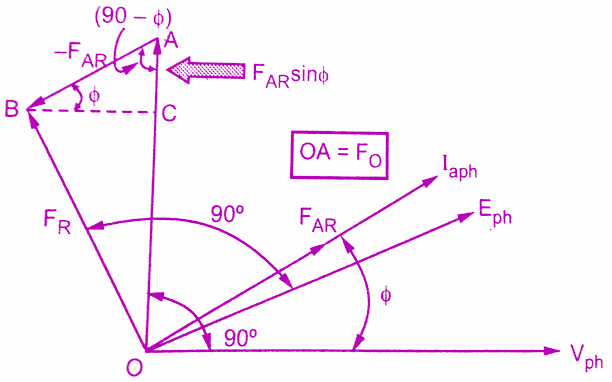
General Case: Now consider that the load power factor is cos Φ. In such case, the resultant MMF is to be determined by vector addition of FO and FAR.
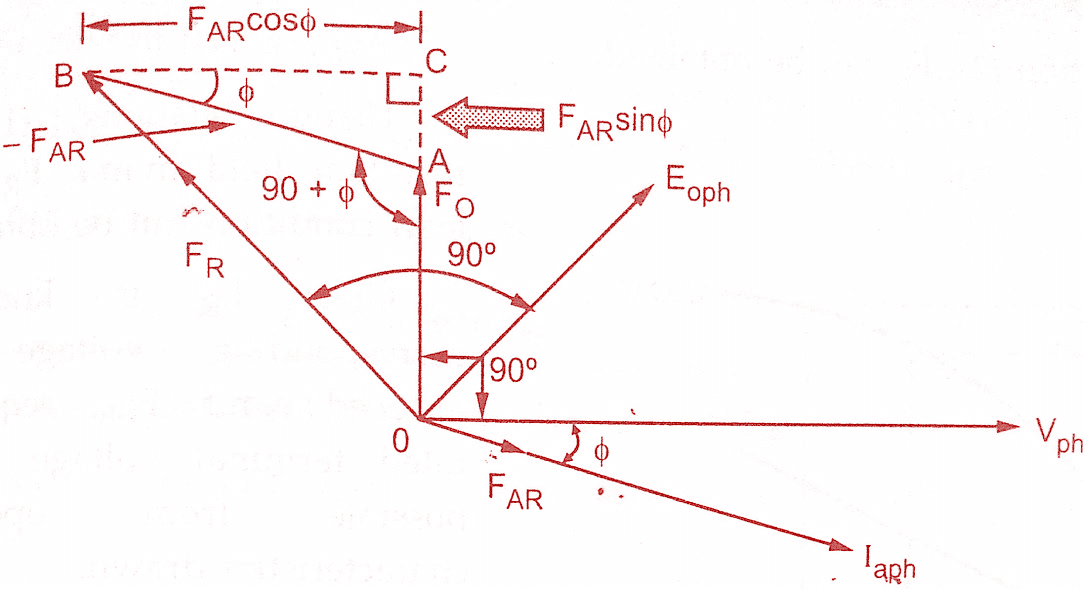
cos Φ, lagging p.f : When the load p.f. is cos Φ lagging, the phase current Iaph lags Vph by angle Φ.The component FO is at right angles to Vph while FAR is in phase with the current Iaph. This is because the armature current Iaph decides the armature reaction. The armature reaction FAR due to current Iaph is to be overcome by field MMF.
Hence while finding resultant field MMF, – FAR should be added to FO vectorially. This is because the resultant field MMF tries to counterbalance armature reaction to produce rated terminal voltage. The phasor diagram of Ampere turn method or MMF method is shown below.
From the phasor diagram the various magnitudes are,
OA = Fo , AB = FAR, OB = FR
Consider triangle OCB which is right angle triangle. The FAR is split into two parts as,
AC = FAR sin Φ and BC= FAR cos Φ
FR = (FO + FAR sin Φ)² + (FAR cos Φ)²
FR can be obtained from the above relation.
Cos Φ, leading p.f : When the load p.f. is cos Φ leading, the phase current Iaph leads Vph by Φ. The component Fo is at right angles to Vph, and FAR is in phase with Iaph. The resultant FR can be obtained by adding FA to Fo. The phasor diagram is shown in the below figure.
From the phasor diagram , various magnitudes are,
AC = FAR sin Φ and BC = FAR cos Φ
OA = FO , AB = FAR and OB = FR
Consider triangle OCB which is right angle triangle.
(OB)² = (OC)² + (BC)²
(FR)² = (FO – FAR sin Φ)² + (FAR cos Φ)²
This textbook “Electrical Machinery by P.S. Bhimbhra” is the best in industry. Grab it now for very less price.
From the relation (2), FR can be obtained,
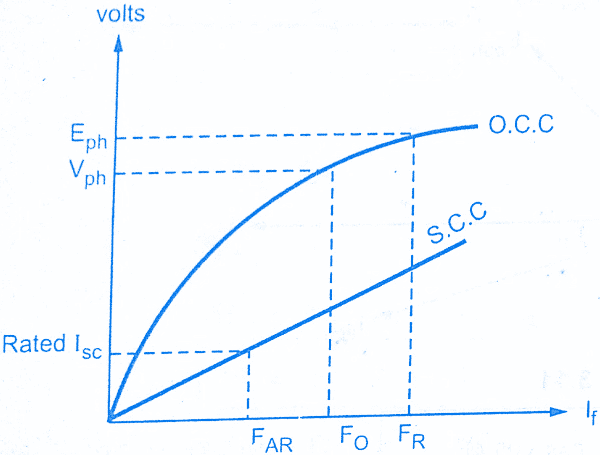
Using relations (1) and (2) resultant field MMF FR for any p.f load condition can be obtained from the above MMF method characteristics diagram.
Once FR is known, obtain a corresponding voltage which induced EMF Eph, required to get rated terminal voltage Vph. This is possible from open circuit characteristics drawn.
Once Eph is known then the voltage regulation can be obtained as,
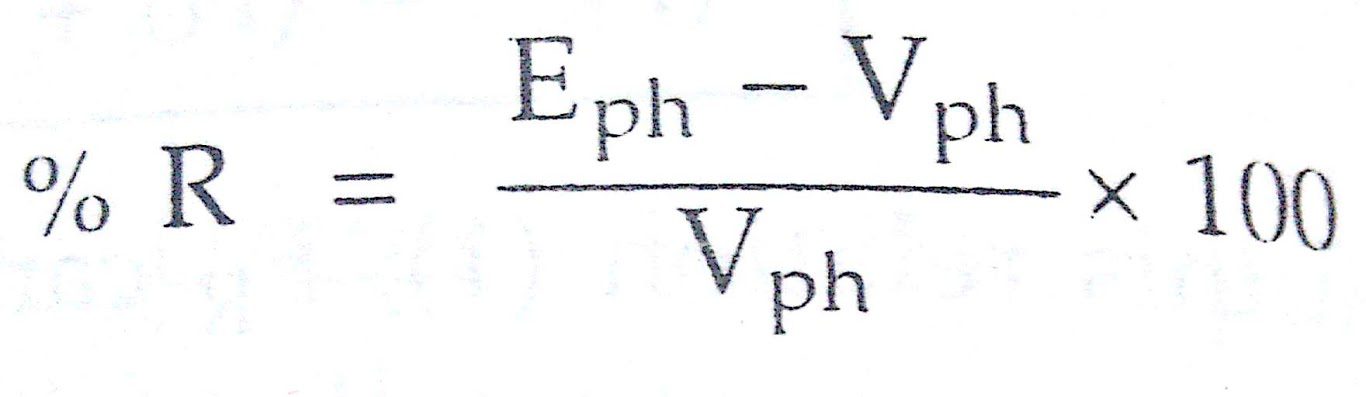
Note : To obtain Eph corresponding to FR O.C.C. must be drawn to the scale, from the open circuit test readings.
Key Point: This ampere turn method gives the voltage regulation of an alternator which is lower than that actually observed. Hence this MMF method is called optimistic method.
Important note: When the armature resistance is neglected then Fo is field mmf required to produce rated Vph at the output terminals. But if the effective armature resistance Raph, is given then Fo is to be calculated from O.C.C. such that Fo represents the excitation (field current) required to produce a voltage of Vph + Iaph Ra cos Φ where
Vph = rated voltage per phase
Iaph = full load current per phase
Ra = armature resistance per phase
cos Φ = power factor of the load
It can also be noted that FR can be obtained using the cosine rule to the triangle formed by Fo, FAR and Fo as shown in the below.
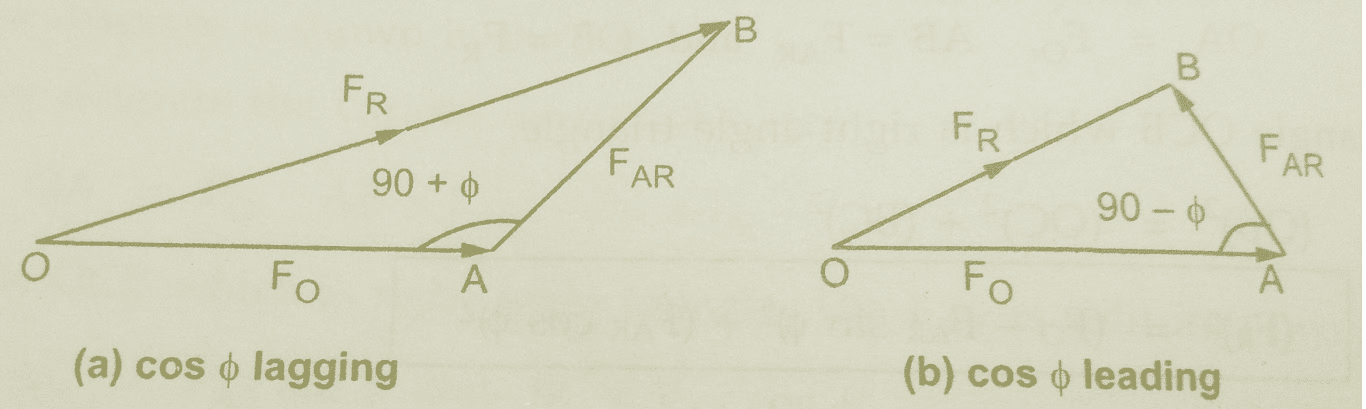
Using cosine rule to triangle OAB,
(FR)² = (FO)² + (FAR)² – 2 FO FAR Cos (FO,FAR)
(FO,FAR) = 90 + Φ if Φ is lagging
= 90 – Φ if Φ is leading
The angle between EO and Vph is denoted as δ and is called power angle. Neglecting Ra we can write,
Ia Xs cos Φ = EO sin δ
Pd = Vph Ia Cos Φ = internal power of the machine
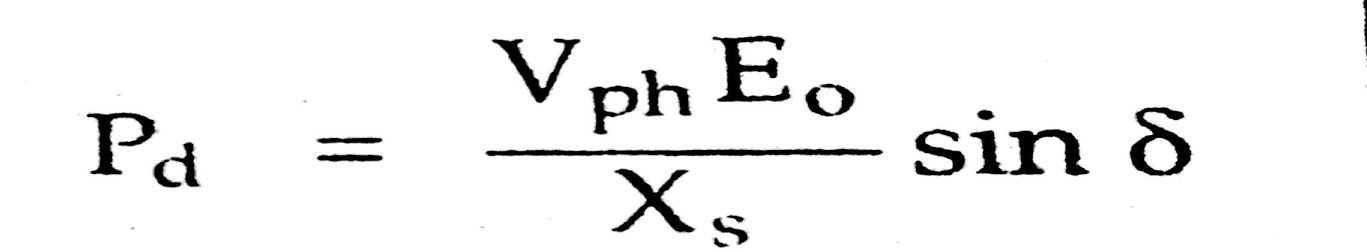
Conclusion:
Now today we have learnt MMF or Ampere turn method for determining voltage regulation of Alternator. You can download this article as pdf, ppt.
Comment below for any Queries.